Science is Life: Refraction of light

Introduction

We know about light and also know that light travels in a straight line path in a medium or two different mediums with same density.
Now a question arises what happens when light travels from one medium to another with different densities for example from air to glass.
When light ray is made to travel from one medium to another say from air to glass medium then light rays bend at the boundary between the two mediums.
So, the bending of light when it passes from one medium to another is called Refraction of light.
The refraction of light takes place on going from one medium to another because the speed of light is different in two media.
Medium in which speed of light is more is called optically rarer medium and medium in which speed of light is less is known as optically denser medium. For example glass is an optically denser medium than air and water.
NOTE:- When light goes from rarer medium to denser medium it bends towards the normal and when it goes from denser medium to rarer medium it bends away from the normal.

Refraction through a rectangular glass slab

To understand the refraction of light through a glass slab consider the figure given below which shows the refraction of light through a rectangular glass slab.
$refraction of light through a rectangular glass slab$
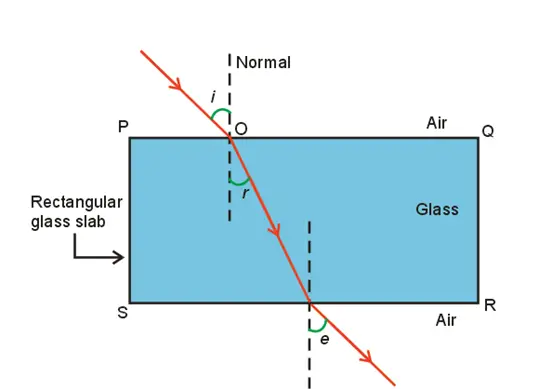
Here in this figure AO is the light ray travelling in air and incident on glass slab at point O.
Now on entering the glass medium this ray bends towards the normal NN’ that is light ray AO gets refracted on entering the glass medium.
After getting refracted this ray now travels through the glass slab and at point B it comes out of the glass slab as shown in the figure.
Since ray OB goes from glass medium to air it again gets refracted and bends away from normalN₁N'₁ and goes in direction BC.
Here AO is the incident ray and BC is the emergent ray and they both are parallel to each other andOB is the refracted ray.
Emergent ray is parallel to incident ray because the extent of bending of the ray of light at the opposite parallel faces which are PQ (air-glass interface) and SR (glass-air interface) of the rectangular glass slab is equal and opposite.
In the figure i is the angle of incidence, r is the angle of refraction and e is the angle of emergence.
Angle of incidence and angle of emergence are equal as emergent ray and incident ray are parallel to each other.
When a light ray is incident normally to the interface of two media then there is no bending of light ray and it goes straight through the medium.

Laws of refraction of light

Refraction is due to change in the speed of light as it enters from one transparent medium to another.
Experiments show that refraction of light occurs according to certain laws.
So Laws of refraction of light are
- The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
If i is the angle of incidence and r is the angle of refraction then sinisinr=constant=n (1)
This constant value is called the refractive index of the second medium with respect to the first.

The Refractive Index

We now know about refraction of light and the extent of the change in direction that takes place in a given pair of media is expressed in terms of the refractive index, the "constant" appearing in equation 1.
The refractive index is related to an important physical quantity that is relative speed of propagation of light in different media as light propagates with different speeds in different media.
Consider the figure given below
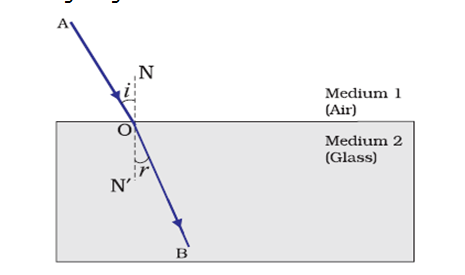
$refraction of liht ray fron rarer medium to denser medium$
Let v₁ be the speed of light in medium 1 and v₂ be the speed of light in medium 2 then the refractive index of medium 2 with respect to medium 1 is given by the ratio of the speed of light in medium 1 and the speed of light in medium 2. So,
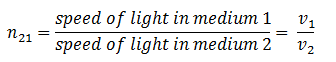
$refractive index of medium 2 with respect to medium 1$
where n₂₁ is the refractive index of medium 2 with respect to medium 1.
The refractive index of medium 1 with respect to medium 2 is represented as n12. It is given by
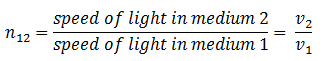
$refractive index of medium 1 with respect to medium 2$
If medium 1 is vacuum or air, then the refractive index of medium 2 is considered with respect to vacuum. This is called the absolute refractive index of the medium.
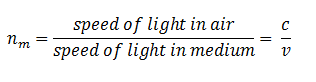
If c is the speed of light in the air and v is the speed of light in any medium then refractive index n_mof the medium would be $refractive index of medium$

Refraction by Spherical Lenses

A lens is a piece of transparent glass bound by two spherical surfaces.
There are two types of lens
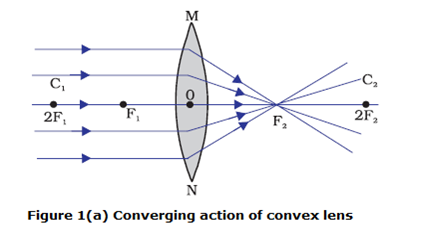
- A convex lens bulges outward and is thick at the center and thinner at the edges. Convex lens converges the light rays as shown below in the figure 1(a).
  
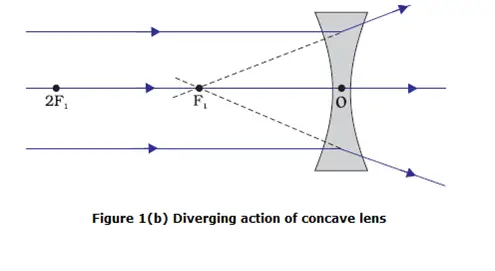
  Hence convex lenses are called converging lenses.
- A concave lens bulges inward and is thinner in the middle and thicker at the edges. Such lenses diverge light rays as shown in Figure 1(b)
  
  Such lenses are called diverging lenses.
A lens, whether it is a convex lens or a concave lens, has two spherical surfaces which form a part of a sphere. The centers of these spheres are called centers of curvature of the lens usually represented by the letter C.
Since there are two centers of curvature, we may represent them as C₁ and C₂.
An imaginary straight line passing through the two centers of curvature of a lens is called its principal axis as shown in figure 1.
The central point of a lens is its optical centre. It is usually represented by the letter O.
A ray of light through the optical centre of a lens passes without suffering any deviation.
The effective diameter of the circular outline of a spherical lens is called its aperture.
In figure 1 (a) you can see several rays of light parallel to the principal axis are falling on a convex lens. These rays, after refraction from the lens, are converging to a point on the principal axis. This point on the principal axis is called the principal focus of the lens.
Letter F is usually used to represent principal focus. A lens has two principal foci.
Similarly in figure 1 (b) several rays of light parallel to the principal axis are falling on a concave lens. These rays, after refraction from the lens, are appearing to diverge from a point on the principal axis. This point on the principal axis is called the principal focus of the concave lens.
The distance of the principal focus from the optical centre of a lens is called its focal length represented by letter f .

Image Formation by Lenses

Lenses form images by refraction of light and type of image formation depends on the position of the object in front of the lens.
We can place the objects at
1. Infinity
2. Beyond 2F₁
3. At 2F₁
4. Between F₁ and 2F₁
5. At focus F₁
6. Between focus F₁ and optical center O

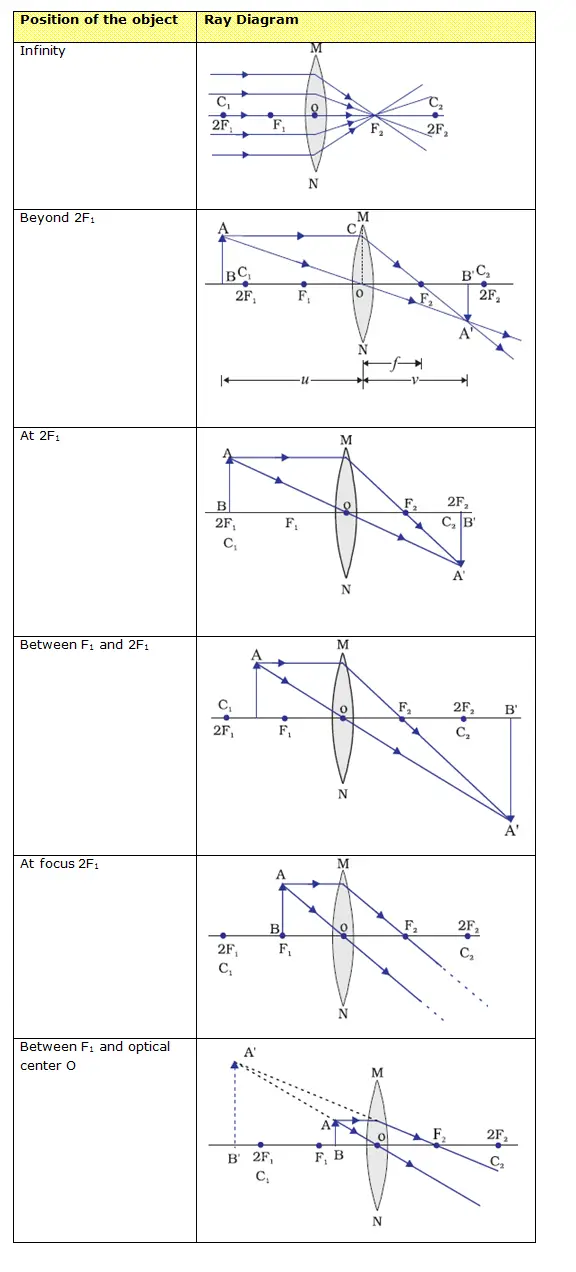
Image formation by a convex lens for different positions of the object is shown below in the table

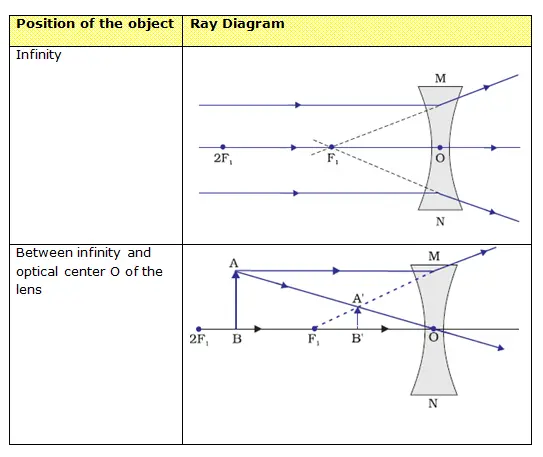
Position of the object	Position of the image	Relative size of the image	Nature of the image
Infinity	At focus F₂	Highly diminished, point sized	Real and inverted
Beyond 2F₁	Between F₂ and 2F₂	Diminished	Real and inverted
At 2F₁	At 2F2	Same size	Real and inverted
Between F₁ and 2F₁	Beyond 2F₂	Enlarged	Real and inverted
At focus 2F₁	At infinity	Infinitely large or highly enlarged	Real and inverted
Between F₁ and optical center O	On the same side of the lens as the object	Enlarged	Virtual and erect

Nature, position and relative size of the image formed by a concave lens for various positions of the object is given below in the table

Position of the object	Position of the image	Relative size of the image	Nature of the image
At infinity	At focus F	Highly diminished, point-sized	Virtual and erect
Between infinity and optical center O of the lens	Between F₁ and optical center O	Diminished	Virtual and erect

A concave lens will always give a virtual, erect and diminished image, irrespective of the position of the object.
Image Formation in Lenses Using Ray Diagrams
- Ray diagram helps us to study the nature, position and relative size of the image formed by lenses.
- For drawing ray diagrams we first consider how light rays falling on both concave and convex lens in three different ways get refracted.
- First consider the case for convex lens
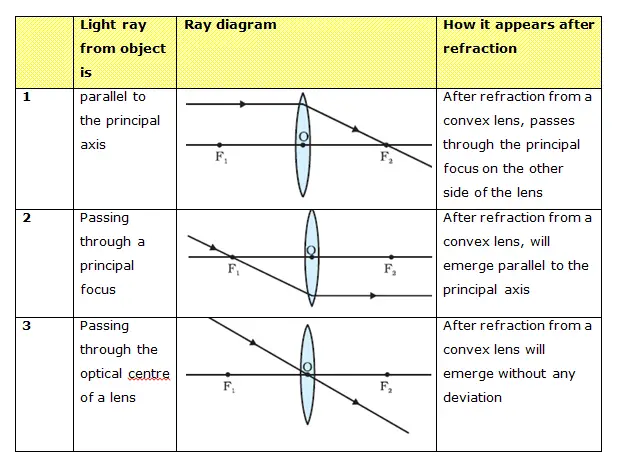
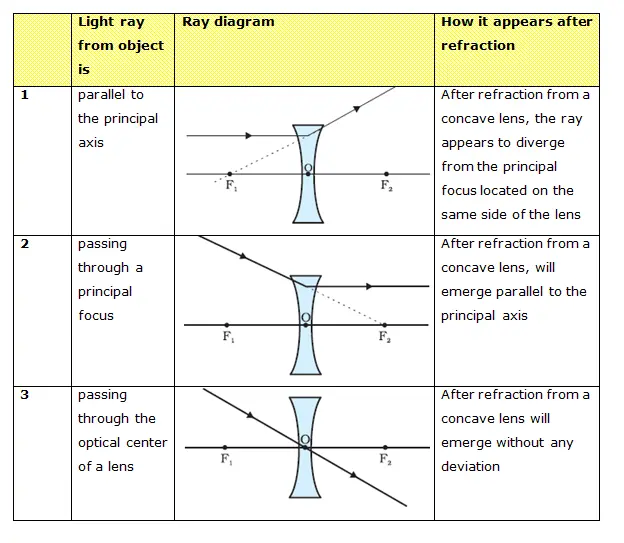
- Secondly consider the case for concave lens
- The ray diagrams for the image formation in a convex lens for a few positions of the object are summarized below in the table
- The ray diagrams for the image formation in a concave lens for a few positions of the object are summarized below in the table
- Sign Convention for Spherical Lenses
  1. All the distances are measured from the optical center of the lens.
  2. The distances measured in the same direction as that of incident light are taken as positive.
  3. The distances measured against the direction of incident light are taken as negative.
  4. The distances measured upward and perpendicular to the principle axis are taken as positive.
  5. The distances measured downwards and perpendicular to principle axis is taken as negative.
  Lens Formula and Magnification
  - Lens Formula gives the relationship between object distance (u), image image-distance (v) and the focal length (f ) and is expressed as
    1f=1v−1u
    This formula is valid in all situations for any spherical lens.
  - The magnification produced by a lens is defined as the ratio of the height of the image and the height of the object.
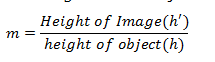
  - Magnification produced by a lens is also related to the object-distance u, and the image-distance v and is given by
    m=vu
  - The power of a lens is defined as the reciprocal of its focal length. It is represented by the letter P. The power P of a lens of focal length f is given by
    P=1f
  - Power of a convex lens is positive and that of a concave lens is negative.
  - The SI unit of power of a lens is ‘dioptre’. It is denoted by the letter D.
  - 1 dioptre is the power of a lens whose focal length is 1 meter so, 1D=1m–1.